◈ 제곱근이란
제곱근을 알기 위해 우선 제곱의 개념을 알아보도록 하겠습니다.
제곱은 같은 수를 두 번 곱했다는 뜻입니다. 2 x 2 또는 3 x 3 처럼 말이죠.
2 x 2 는 2의 제곱이라고 부르고 지수를 이용해 다음과 같이 표현합니다.

3 x 3 은 3의 제곱이라 부르며 역시 지수로 표현할 수 있습니다.


제곱근을 이해하기 위해서는 제곱의 개념을 거꾸로 생각해보면 됩니다.
즉, a라는 수를 제곱했을 때(두 번 곱했을 때) b라는 수가 나온다면, b의 제곱근은 a가 되는 것입니다.
예를 들어 4의 제곱근이 무엇인가?라고 물어본다면, 동일한 크기의 수를 두 번 곱해서 4가 나오는 경우는 2 또는 -2 가 있으므로 '4의 제곱근은 2 또는 -2다'라고 할 수 있습니다.

◈ 루트(=제곱근)
제곱근이라는 말과 동일한 의미로 쓰이는 단어로 '루트'가 있습니다. 영어에서 뿌리라는 뜻을 가진 'root'입니다.
'4의 제곱근'을 '루트 4'라고 부르기도하며, 다음과 같이 표기 합니다.

4 앞에 위치한 체크 표시 비슷한 꺽쇠 모양의 기호를 우리는 '근호'라고 부르며, 선생님들은 수업 중에 '근호를 씌운다'라는 표현을 자주 하실 겁니다.
예를 들어, '4에 근호를 씌운다'라는 표현은 '4의 제곱근을 구한다'라는 말과 같은 의미이므로 당황하지 않아도 됩니다.

◈ 음의 제곱근
앞서 4의 제곱근이 2 또는 -2라고 했습니다. 2 x 2 = 4, -2 x -2 =4 이기 때문이지요.
이처럼 어떤 수의 제곱근은 양수와 음수 두 가지이며, 양수인 제곱근을 양의 제곱근, 음수인 제곱근을 음의 제곱근이라고 부릅니다.제곱근에는 음의 제곱근이 있다는 것을 놓치면 안 됩니다.이를 노리는 문제가 종종 출제되기 때문입니다.
◈ 제곱과 제곱근 그리고 정사각형
정사각형을 이용하면 제곱과 제곱근을 시각화해서 이해할 수도 있습니다. 제곱과 제곱근의 관계를 정사각형의 넓이와 한 변의 길이 관계로 생각해 볼 수 있습니다.
한 변이 3인 정사각형의 넓이는 3 x 3 = 9 입니다. 그렇다면 넓이가 9인 정사각형의 한 변 길이는 무엇일까요? 3이 되겠지요. 이처럼 정사각형 한 변의 길이를 제곱하여 넓이를 구하고, 정사각형 넓이의 제곱근을 구해(정사각형 넓이에 루트를 씌워서) 한 변의 길이를 알아낼 수 있습니다.

◈ 제곱근표
정수로 딱 떨어지는 제곱근들은 계산하는 데 어려움이 없습니다. 하지만 2나 3 또는 5의 제곱근은 어떻게 계산할까요? 계산이 불가능합니다. 반복되지 않는 무한 소수이기 때문입니다. 예를 들면 2의 제곱근은 1.414......, 3의 제곱근은 1.732......, 5의 제곱근은 2.236.....입니다.
제곱근 계산에 난항을 겪을 우리를 위해 '제곱근표'라는 것이 있습니다. 제곱근을 소수 셋째 자리까지 표현하여 모아놓은 표라고 보면 되겠습니다. <제곱근표 링크>
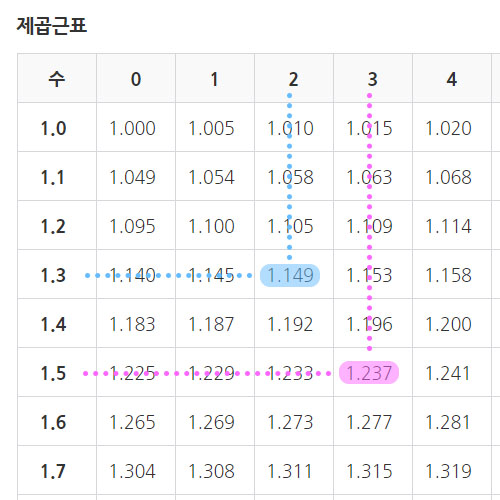
제곱근표를 보는 방법은, 가령 1.32의 제곱근을 구하고 싶으면, 제곱근표의 가장 왼쪽 세로열과 가장 위쪽 가로 열을 조합하여 1.32가 되는 교차점의 수를 찾으면 됩니다. 1.32의 제곱근은 1.149입니다.
마찬가지로 1.53의 제곱근은 1.237이 됩니다.
제곱근표에 나오는 소수들을 모두 외울 필요는 없습니다. 문제에서 대부분 주어지기 때문입니다. 하지만 2의 제곱근, 3의 제곱근, 5의 제곱근 정도는 기억해 두고 있다면 문제 풀이에 도움이 될 때가 있습니다. 제곱근 관련 문제를 많이 풀다 보면 저절로 외워지니 너무 부담은 갖지 않아도 됩니다.
지금까지 중 3 수학에서 다루는 제곱근(루트)에 대해 알아보았습니다.
수학 문제는 다양한 유형의 문제를 많이 풀어보는 것이 중요합니다. 유형을 익히기 위해서이기도 하지만, 반복적인 문제 풀이 훈련을 통해 시간을 단축해야 할 필요성도 있기 때문입니다.
그렇기 때문에, 지금 참고 하고 있는 문제집이나 참고서 말고도 좀 더 많은 교제들을 풀어봐야겠습니다.
더욱이 제곱근(루트)은 고등학교에 올라가서도 자주 쓰기 때문에 개념에 대한 이해를 반드시 해 두어야 하겠습니다.
+ 더 읽어볼 만한 이야기
중 3 수학: 이차방정식, 근의 공식을 용한 이차방정식 문제 푸는 방법
◈ 이차방정식이란 이차방정식은 미지수의 차수가 2인 방정식을 의미합니다. 기본적인 형태는 다음과 같습니다. a가 0이 아니어야 하는 이유는, a가 0일 경우 위의 식은 더 이상 2차 방정식이 아
summarizor.tistory.com
'학습' 카테고리의 다른 글
| 중 1 수학: 부채꼴의 넓이 공식. 호의 길이 구하는 공식 (0) | 2021.01.23 |
|---|---|
| 중 2 수학: 연립방정식. 연립방정식 푸는 법 (2) | 2021.01.20 |
| 중 1 수학: 일차방정식. 일차방정식 문제 풀이 방법 (0) | 2021.01.14 |
| 중 1 수학: 방정식이란? 등식, 미지수 그리고 방정식의 해, 근 (0) | 2021.01.12 |
| 중학교 2학년 수학: 순환소수. 순환소수를 분수로 고치는 방법 (0) | 2021.01.08 |




댓글